I began investigating the interplay between machine learning and physics—primarily for modeling spatio-temporal dynamics—in 2017, through a collaboration with physicist colleagues (M. Lévy, G. Gastineau, and S. Thiria) at the LOCEAN laboratory at Sorbonne University. Since then, I have developed several additional collaborations, including work with colleagues from INRIA Paris (notably J. Salomon, INRIA/ANGE) and INRIA Sophia (M. Sermesant, INRIA/Épione) within the DeepNum project, which focuses on the numerical analysis of ML solvers. I have also collaborated with P. Cinnella and T. Sayadi on research at the interface of machine learning and fluid dynamics.
I was awarded an AI Chair in 2019 – a national program from France AI strategy. The project is entitled « DL4CLIM: Deep Learning for Physical Processes ». The program will run until 2026. It is managed by french ANR, you will find the announcement page on the ANR site here.
Together with P. Cinnella from d’Alembert Lab at Sorbonne and and T. Sayadi Taraneh Sayadi from CNAM Paris as co-PIs, we were awarded the AI Chair “Deep Learning for Science: Modeling Fluid Dynamics in Engineering and Climate Physics” (2025–2030), as part of the PostGenAI@Paris AI cluster at Sorbonne University, under the France 2030 plan.
In the MLIA team, we have been mainly exploring the following issues:
- How to incorporate prior physical knowledge in machine learning models
How to leverage both prior physical background on a phenomenon and information extracted from data? How can ML models come as a complement to physical ones?
- Domain generalization
When physical models are valid on whole domains, e.g. whole oceans, ML models do not generalize outside their training domain. When trained on physical data they do not capture the underlying laws of nature and do not generalize to other contexts (space or time). This is a major limitation of data based approaches to physics.
- Operator learning
Learning mappings between function spaces, leading to continuous spatio-temporal representations. The objective is to get space/ time resolution independent or mesh free models of the dynamics.
- Foundation models
We have also started to explore foundation models for multiphysics.
Tutorial on physics-aware deep learning
- Here is a tutorial at ECML 2023 – partly outdated now
Recent publications related to the topic of the chair at MLIA
- See my page on DPLP or Scholar
- Here are a few links on recent publications
- Koupaï, A. K., le Boudec, L., Serrano, L., & Gallinari, P. (2025). ENMA: Tokenwise Autoregression for Generative Neural PDE Operators. NeurIPS.
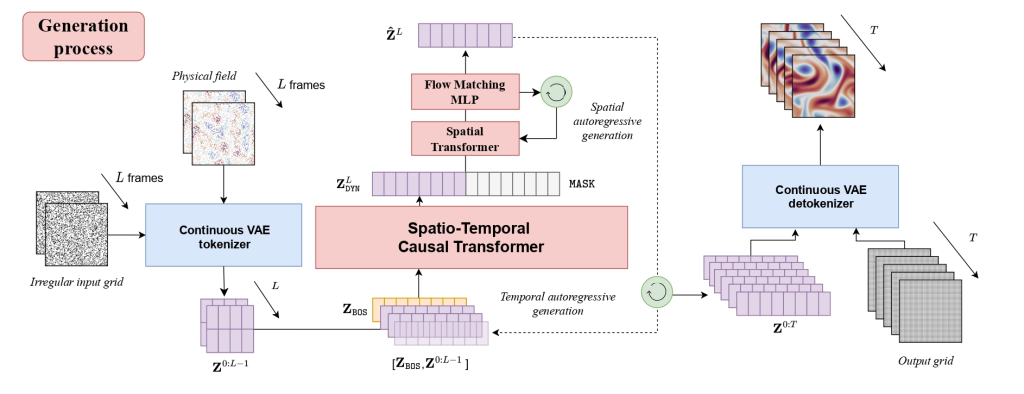
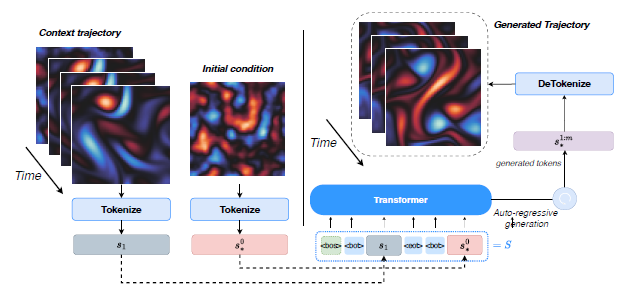
- Serrano, L., Kassaı Koupai, A., Wang, T. X., Erbacher, P., & Gallinari, P. (2025). Zebra: In-Context Generative Pretraining for Solving Parametric PDEs. ICML.
- le Boudec, L., de Bezenac, E., Serrano, L., Daniel Regueiro-Espino, R., Yin, Y., & Gallinari, P. (2025). Learning a Neural Solver for Parametric PDEs to Enhance Physics-Informed Methods. ICLR.
https://github.com/2ailesB/neural-parametric-solver. - Kassai Koupai, A., Benet, J. M., Yin, Y., Vittaut, J.-N., & Gallinari, P. (2024). GEPS: Boosting Generalization in Parametric PDE Neural Solvers through Adaptive Conditioning.NeurIPS. https://geps-project.github.io/
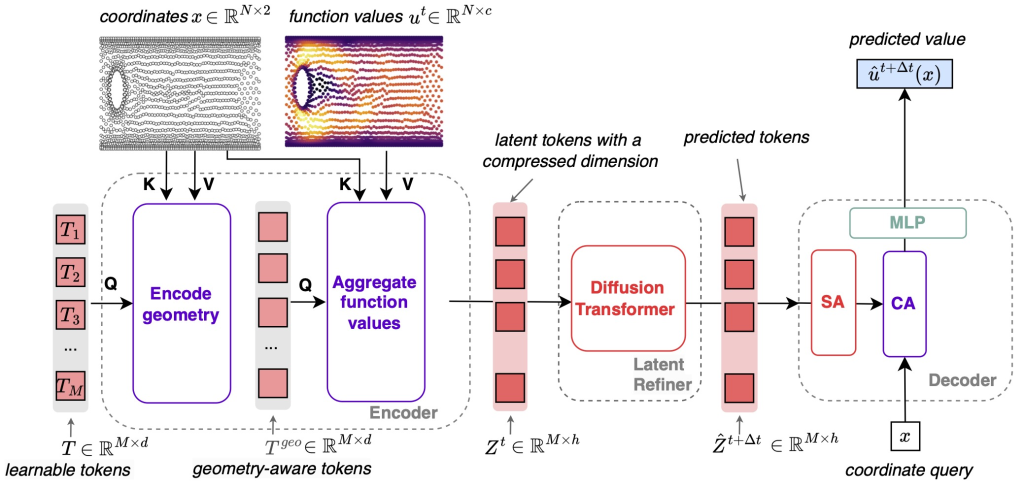
- Serrano, L., Wang, T., le Naour, E., Vittaut, J.-N., & Gallinari, P. (2024). AROMA : Preserving Spatial Structure for Latent PDE Modeling with Local Neural Fields. NeurIPS.
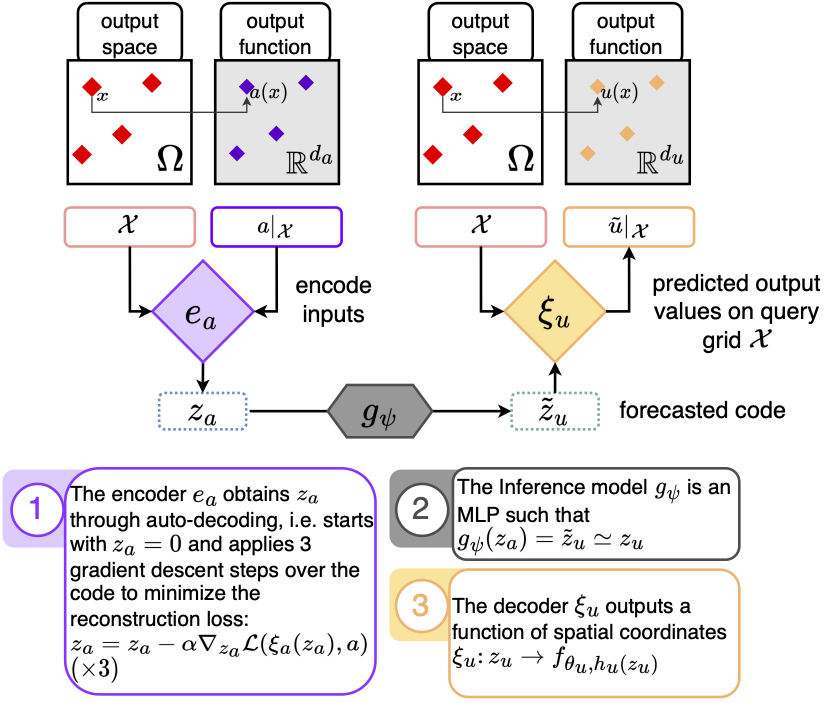
- Serrano, L., Boudec, L. le, Koupaï, A. K., Wang, T. X., Yin, Y., Vittaut, J.-N., & Gallinari, P. (2023). Operator Learning with Neural Fields: Tackling PDEs on General Geometries. NeurIPS. http://arxiv.org/abs/2306.07266
PhD manuscripts and theses for which I served as advisor or co-advisor
… including several interdisciplinary theses co-supervised with colleagues in applied mathematics, climate science, and fluid dynamics.
-
- Arthur Pajot -2019- Incorporating physical knowledge into deep neural network
- Emmanuel de Bezenac – 2021- Modeling Physical Processes with Deep Learning: A Dynamical Systems Approach
- Jérémie Donà – 2022 – Statistical Learning of Physical Dynamics
- Ibrahim Ayed – 2022 –Neural Models for Learning Real World Dynamics and the Neural Dynamics of Learning
- Marie Dechelle-Marquet – 2023 – Deep learning based physical-statistics modeling of ocean dynamics
- Matthieu Kirchmeyer – 2023 – Out-of-Distribution Generalization in Deep Learning: Classification and Spatiotemporal Forecasting
- Yuan Yin – 2023 – Physics-Aware Deep Learning and Dynamical Systems : Hybrid Modeling and Generalization
- Victoriya Kashtanova – 2023 – Learning cardiac electrophysiology dynamics with PDE-based physiological constraints for data-driven personalised predictions
- Léon Migus – 2023 – Deep neural networks and partial differential equations
- Louis Serrano – 2025 – Operator learning for modeling spatiotemporal dynamics from PDEs